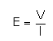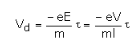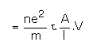Write assumptions of free electron theory of metals & how using free electron theory Ohm's law can be deduced.

A metal is imagined as the structure of 3-dimensional array of ions in between which, there are free moving valence electrons confined to the body of the material. Such freely moving electrons cause electrical conduction under an applied field and hence referred to as conduction electrons. The free electrons are treated as equivalent to gas molecules and they are assumed to obey the laws of kinetic theory of gases. In the absence of the field, the energy associated with each electron at a temperature T is given by 3/2 kT, where k is a Boltzmann constant. It is related to the kinetic energy. 3/2 kT = ½ mvth^2 Where vth is the thermal velocity same as root mean square velocity. The electric potential due to the ionic cores is taken to be essentially constant throughout the body of the metal and the effect of repulsion between the electrons is considered insignificant. The electric current in a metal due to an applied field is a consequence of the drift velocity in a direction opposite to the direction of the field.

To find the relationship between current and drift velocity, consider a conductor of length l and area of cross-section A. If V is the potential difference across the ends of the conductor, then the strength of the electric field is 

The acceleration acquired by each electron due to the electric field is

where 

is the coulomb’s force experienced by each electron and m is the mass of the electron.

The drift velocity of the electrons is given by 

where t, the relaxation time, is the average time that an electron spends between two collisions. It is of the order of 10-14 s.

Now the volume of the conductor is equal to Al and if n is the number of free electrons per unit volume, then, the total number of free electrons in the conductor will be equal to n Al.

Hence, the total charge q = - n Ale

The time taken by free electrons to cross the conductor is

where we have substituted for t and q.

For a given conductor, I a Vd

A small value of drift velocity 10-5m/sec produces a large amount of current, as there are a large number of free electrons in a conductor.

The drift velocity of the electrons Vd is (using E = V / l)

Also I = - neAVd

On substituting for Vd in the above expression we get,

or

Which shows that current is directly proportional to the applied voltage(Ohm’s law).From this, the resistance R can be identified as